Crack the 11+ Maths Exam: Proven Strategies to Conquer Fractions with Confidence!

Fractions are a key topic in the 11+ Maths Exam, often appearing in calculations, problem-solving, and real-world scenarios. Many students find them tricky, but with the right strategies, fractions can become one of the easiest topics to master.

In this guide, we’ll break down essential fraction concepts and provide proven methods to help students tackle fraction problems with confidence.

Why Are Fractions Important in the 11+ Maths Exam?

Fractions appear in many question types, including:

• Basic operations – Adding, subtracting, multiplying, and dividing fractions.
• Word problems – Applying fractions in real-life situations.
• Comparing and ordering – Understanding which fraction is greater or smaller.
• Conversions – Changing fractions into decimals and percentages.
• Problem-solving – Using fractions in multi-step calculations.

Since fractions form the foundation of many advanced maths topics, mastering them is essential for success in the 11+ Maths Exam.

Step 1: Understanding the Basics

A fraction represents a part of a whole and consists of two numbers:

• Numerator (top number): Shows how many parts are taken.
• Denominator (bottom number): Indicates the total number of equal divisions in a whole.

For example, in 3/5, the numerator (3) means three parts are considered, while the denominator (5) tells us the whole is divided into five equal parts.

Types of Fractions

• Proper Fractions: A fraction where the numerator is less than the denominator (e.g., 4/9).
• Improper Fractions: Numerator is greater than or equal to the denominator (e.g., 7/5).
• Mixed Numbers: A whole number combined with a fraction (e.g., 2 ⅓).

Recognising these types is essential before moving on to fraction operations.

Step 2: Simplifying Fractions for Quick Calculations

Simplifying fractions makes calculations easier and ensures answers are in their simplest form.

Example: Simplify 24/36

Find the Greatest Common Factor (GCF) of 24 and 36.
The GCF is 12.
Divide both by 12:

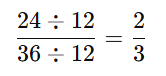
Final Answer: 2/3

Simplifying fractions helps speed up calculations during the exam.

Step 3: Adding and Subtracting Fractions the Easy Way

Fractions need a common denominator before they can be added or subtracted.

Steps to Add or Subtract Fractions:

• Identify the Least Common Denominator (LCD).
• Adjust fractions so they have the same denominator.
• Add or subtract the numerators.
• Simplify the answer if needed.

Example: 1/6 + 1/4

• The LCD of 6 and 4 is 12.
• Convert: 1/6 = 2/12, 1/4 = 3/12.
• Add: 2/12 + 3/12 = 5/12.

Final Answer: 5/12

The same process applies to subtraction.

Step 4: Multiplying and Dividing Fractions with Ease

Multiplication Rule: Multiply numerators and denominators directly.

Division Rule: Flip (reciprocal) the second fraction and then multiply.

Example 1: Multiplication

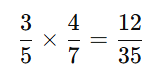
Example 2: Division

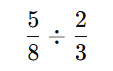
Flip 2/3 to 3/2.

Now multiply:

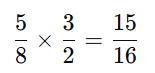
Final Answer: 15/16

Step 5: Converting Fractions to Decimals and Percentages

Fractions can be rewritten as decimals or percentages for easier interpretation.

• Fraction → Decimal: Divide the numerator by the denominator.
• Fraction → Percentage: Convert to decimal, then multiply by 100.

Example: Convert 3/8 to a Percentage

• 3 ÷ 8 = 0.375
• 0.375 × 100 = 37.5%

Final Answer: 37.5%

Step 6: Comparing and Ordering Fractions

Fractions can be compared by either:

• Converting to a common denominator
• Changing them into decimals

Example: Arrange 2/9, 3/5, and 4/7 in Ascending Order

Convert to decimals:

• 2/9 = 0.222
• 3/5 = 0.6
• 4/7 = 0.571

Order from smallest to largest: 2/9 < 4/7 < 3/5

Step 7: Solving Word Problems with Fractions

Fractions are frequently tested in real-life problems during the 11+ Maths Exam.

Example Problem:

A cake is cut into 8 equal slices. If Emma eats 3 slices and her friend eats 2 slices, what fraction of the cake remains?

• Total slices = 8
• Slices eaten = 3 + 2 = 5
• Remaining slices = 8 – 5 = 3

Final Answer: 3/8 of the cake remains.

Top Strategies for Mastering Fractions in the 11+ Maths Exam

• Understand fraction basics – A strong foundation makes problem-solving easier.
• Practise different operations – Addition, subtraction, multiplication, and division require different methods.
• Use estimation – It helps check if answers make sense.
• Simplify when possible – Smaller numbers make calculations easier.
• Solve practice questions – The more you practise, the better you get.

Applying these strategies will help students develop confidence and accuracy when working with fractions.

For more in-depth learning, check out Avidator’s 11+ Maths Series, designed to simplify tricky maths topics.

Final Thoughts

Fractions don’t have to be overwhelming. By breaking down concepts step by step, practising regularly, and using smart strategies, students can approach fraction questions with confidence in the 11+ Maths Exam.